목차

재귀 함수

재귀 함수는 문제를 해결하기 위해 자신을 호출하여 문제를 더 작은 하위 문제로 나누는 함수입니다. 문제를 해결하는 프로세스에는 기본 사례 또는 중지 조건에 도달할 때까지 반복되는 자체 호출이 포함되며, 이 시점에서 함수는 자신을 다시 호출하지 않고 결과를 반환합니다. 재귀 함수는 특정 문제를 해결하는 우아하고 간결한 방법일 수 있지만 신중하게 구현하지 않으면 성능 문제나 스택 오버플로 오류가 발생할 수도 있습니다.

다음은 숫자의 펙토리얼을 계산하는 재귀 함수의 예입니다.

def factorial(n):
    if n == 0 or n == 1:
        return 1  # Base case
    else:
        return n * factorial(n - 1)  # Recursive call

result = factorial(5)
print(result)  # Output: 120

이 예에서 factorial 함수는 인수 n - 1로 자신을 호출하여 숫자 n의 펙토리얼을 계산합니다. 기본 사례는 n이 0 또는 1인 경우이며, 이 경우 함수는 자신을 다시 호출하지 않고 1을 반환합니다. 'n'의 펙토리얼은 기본 케이스에 도달할 때까지 'n'에 'n - 1'의 펙토리얼 등을 곱하여 계산됩니다.

재귀 프로세스를 더 잘 이해하기 위해 factorial(5)의 계산을 살펴보겠습니다.

factorial(5) = 5 * factorial(4)
factorial(4) = 4 * factorial(3)
factorial(3) = 3 * factorial(2)
factorial(2) = 2 * factorial(1)
factorial(1) = 1(기본 케이스)

함수 호출은 역순으로 해결됩니다.

factorial(2) = 2 * 1 = 2
factorial(3) = 3 * 2 = 6
factorial(4) = 4 * 6 = 24
factorial(5) = 5 * 24 = 120

재귀 함수를 사용할 때 스택 오버플로 오류로 이어질 수 있는 무한 재귀를 피하기 위해 기본 사례 또는 중지 조건을 정의하는 것이 중요합니다. 또한 일부 문제는 성능 문제로 인해 재귀에 적합하지 않을 수 있으며 이 경우 반복 솔루션이 더 적합할 수 있습니다.

팩토리얼을 구현하는 2가지 방법

1. 루프 사용(반복 방법)
반복 방법에는 루프를 사용하여 주어진 숫자의 팩토리얼을 계산하는 것이 포함됩니다. for 루프를 사용하여 각 정수를 1에서 n까지 곱할 수 있습니다.

def factorial_iterative(n):
    result = 1
    for i in range(1, n + 1):
        result *= i
    return result

n = 5
result = factorial_iterative(n)
print(f"{n}! = {result}")  # Output: 5! = 120

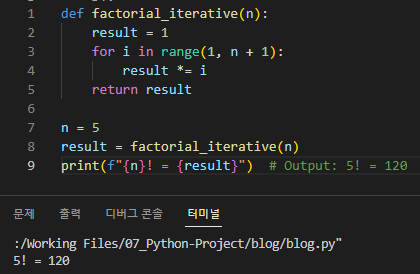
이 예제에서는 정수 n을 입력으로 사용하는 factorial_iterative 함수를 정의합니다. 이 함수는 변수 result를 1로 초기화한 다음 for 루프를 사용하여 1에서 n(포함)까지 반복합니다. 각 반복에서 루프 변수 i는 result의 현재 값과 곱해져 값이 업데이트됩니다.


2. 재귀 함수 사용
재귀 함수는 문제를 해결하기 위해 자신을 호출하여 문제를 더 작은 하위 문제로 나누는 함수입니다. 재귀를 사용하여 n = 0 또는 n = 1(0! = 1! = 1이므로)에 대한 기본 사례를 사용하여 숫자의 팩토리얼을 계산할 수 있습니다. 아래 예시는 처음 보여드렸던 팩토리얼 예시와 동일합니다.

def factorial_recursive(n):
    if n == 0 or n == 1:
        return 1  # Base case
    else:
        return n * factorial_recursive(n - 1)  # Recursive call

n = 5
result = factorial_recursive(n)
print(f"{n}! = {result}")  # Output: 5! = 120

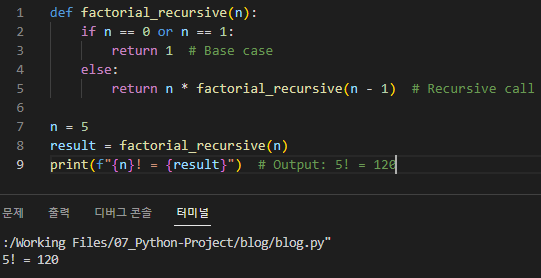
이 예에서 factorial_recursive 함수는 인수 n - 1로 자신을 호출하여 숫자 n의 팩토리얼을 계산합니다. 기본 사례는 n이 0 또는 1인 경우이며, 이 경우 함수는 자신을 다시 호출하지 않고 1을 반환합니다. 'n'의 팩토리얼은 기본 케이스에 도달할 때까지 'n'에 'n - 1'의 팩토리얼 등을 곱하여 계산됩니다.

두 방법 모두 숫자의 팩토리얼을 계산하는 데 사용할 수 있지만 일반적으로 반복 방법이 더 효율적이고 큰 n 값에 대한 스택 오버플로 오류가 덜 발생합니다. 반면에 재귀 방법은 일부 사람들에게 더 우아하고 이해하기 쉬울 수 있습니다.

피보나치 수열

피보나치 수열은 처음 두 수 이후의 각 숫자가 앞의 두 숫자의 합인 일련의 숫자입니다. 수열은 일반적으로 0과 1로 시작하며 다음과 같이 진행됩니다.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

수학적 용어로 피보나치 수열은 다음과 같은 점화식으로 정의됩니다.

F(n) = F(n-1) + F(n-2)

초기 조건: 

F(0) = 0, F(1) = 1

피보나치 수열을 재귀 함수로 구현하려면 정수 n을 입력으로 받고 n번째 피보나치 숫자를 반환하는 함수를 만듭니다. 함수는 인수 n-1 및 n-2로 자신을 호출한 다음 결과를 합산하여 n번째 피보나치 숫자를 계산합니다. 함수의 기본 경우는 n이 0 또는 1인 경우로, 이 경우 해당 피보나치 숫자를 직접 반환합니다.

n번째 피보나치 숫자를 찾기 위한 재귀 함수의 예는 다음과 같습니다:

def fibonacci_recursive(n):
    if n == 0:
        return 0  # 기본 경우: F(0) = 0
    elif n == 1:
        return 1  # 기본 경우: F(1) = 1
    else:
        return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)  # 재귀 호출

n = 10
result = fibonacci_recursive(n)
print(f"Fibonacci({n}) = {result}")  # 출력: Fibonacci(10) = 55

이 예제에서 fibonacci_recursive 함수는 위에서 언급한 점화식을 사용하여 n번째 피보나치 숫자를 계산합니다. 함수는 n이 0 또는 1과 같은 기본 경우를 가지며, 다른 n 값에 대해 자신을 재귀적으로 호출합니다.

이 재귀 구현은 n의 값이 커질수록 상당히 느려지고 비효율적이 될 수 있다는 점에 유의해야 합니다. 이 경우 반복 루프, 메모이제이션 또는 행렬 거듭제곱과 같은 대안 방법을 사용하여 성능을 개선할 수 있습니다.

다음은 재귀 함수 코드를 작성하면서 발생할 수 있는 일반적인 실수와 그 예시입니다.

1. 베이스 케이스 누락: 재귀 함수를 작성할 때 고려해야 하는 첫 번째 것은 베이스 케이스입니다. 베이스 케이스는 재귀 호출이 종료되는 조건을 정의합니다. 이를 빼먹으면 함수가 무한정 자기 자신을 호출하게 되어 스택 오버플로우가 발생할 수 있습니다.

   예시:

  def factorial(n):
       # 베이스 케이스 누락
       return n * factorial(n - 1)

   수정:

   def factorial(n):
       if n == 0:  # 베이스 케이스
           return 1
       return n * factorial(n - 1)

 
2. 잘못된 베이스 케이스: 잘못된 베이스 케이스를 정의하면 예상치 못한 결과 또는 런타임 오류가 발생할 수 있습니다.

   예시:

   def factorial(n):
       if n == 1:  # 잘못된 베이스 케이스
           return 0
       return n * factorial(n - 1)

   
   수정:

   def factorial(n):
       if n == 0:  # 올바른 베이스 케이스
           return 1
       return n * factorial(n - 1)

   
3. 재귀 호출을 빼먹는 것: 재귀 함수는 수정된 인수로 자기 자신을 호출해야 합니다. 재귀 호출을 빼먹으면 함수가 예상한 대로 동작하지 않을 수 있습니다.

   예시:

   def sum_natural_numbers(n):
       if n == 1:
           return 1
       # 재귀 호출을 빼먹음

   수정:

   def sum_natural_numbers(n):
       if n == 1:
           return 1
       return n + sum_natural_numbers(n - 1)  # 재귀 호출

4. 재귀 호출용 인수를 업데이트하지 않는 것: 재귀 호출할 때 함수가 베이스 케이스로 수렴하도록 인수를 올바르게 수정해야 합니다.

   예시:

   def factorial(n):
       if n == 0:
           return 1
       return n * factorial(n)  # 인수를 업데이트하지 않음

   수정:

   def factorial(n):
       if n == 0:
           return 1
       return n * factorial(n - 1)  # 인수를 올바르게 업데이트

목차

1. 리턴 값
2. 다양한 사용 예시
3. 자주 발생하는 실수들

리턴 값

Python에서 리턴 값은 함수가 호출될 때 생성된 출력 또는 결과입니다. 리턴 값은 숫자, 문자열, 목록, 튜플, 사전 또는 사용자 지정 개체와 같은 모든 데이터 유형이 될 수 있습니다. Python의 함수는 return 문이 지정되지 않은 경우 암시적으로 None을 반환합니다. 

함수에서 값을 반환하려면 return 키워드 다음에 반환하려는 값이나 표현식을 사용하십시오. 'return' 문이 실행되면 함수가 종료되고 리턴 값이 호출자에게 다시 전송됩니다.

다음은 리턴 값의 개념을 설명하는 예입니다.

def add_numbers(a, b):
    result = a + b
    return result

# 함수 호출 및 반환 값을 변수에 저장
sum_result = add_numbers(3, 5)
print(sum_result)  # Output: 8

이 예에서 add_numbers 함수는 두 개의 매개변수 a 및 b를 사용하여 합계를 계산하고 return 문을 사용하여 결과를 반환합니다. 함수가 호출되면 리턴 값이 sum_result 변수에 저장되어 출력됩니다. 함수는 여러 값을 튜플로 반환할 수도 있습니다. 예를 들면 다음과 같습니다.

def calculate_area_and_perimeter(length, width):
    area = length * width
    perimeter = 2 * (length + width)
    return area, perimeter

# 함수 호출하고 반환 값을 변수에 저장
area_result, perimeter_result = calculate_area_and_perimeter(10, 5)
print(f"Area: {area_result}, Perimeter: {perimeter_result}")  # Output: "Area: 50, Perimeter: 30"

이 예에서 calculate_area_and_perimeter 함수는 직사각형의 면적과 둘레라는 두 가지 값을 반환합니다. 함수가 호출되면 리턴 값은 area_result 및 perimeter_result 변수에 저장됩니다. 

return 문이 실행되면 함수가 즉시 종료된다는 점을 기억해야 합니다. 함수 내에서 return 문 뒤에 오는 코드는 실행되지 않습니다.

다양한 사용 예시

1. 단일 값 반환: return 키워드의 가장 일반적인 용도는 함수에서 숫자, 문자열 또는 부울과 같은 단일 값을 반환하는 것입니다.

def square(x):
    return x * x

result = square(4)
print(result)  # Output: 16

2. 여러 값 반환: 함수는 튜플을 사용하여 여러 값을 반환할 수 있으며 호출자는 이를 별도의 변수로 풀 수 있습니다.

def get_name_and_age():
    return "Alice", 30

name, age = get_name_and_age()
print(name, age)  # Output: Alice 30

3. 목록, 사전 또는 기타 데이터 구조 반환: 함수는 목록, 사전, 집합 또는 사용자 지정 개체와 같은 보다 복잡한 데이터 구조를 반환할 수 있습니다.

def get_squares(numbers):
    return [x * x for x in numbers]

squares = get_squares([1, 2, 3, 4])
print(squares)  # Output: [1, 4, 9, 16]

4. 함수 또는 람다 함수 반환: 함수는 변수에 할당하고 나중에 호출할 수 있는 다른 함수 또는 람다 함수를 반환할 수 있습니다.

def make_multiplier(factor):
    return lambda x: x * factor

double = make_multiplier(2)
print(double(5))  # Output: 10

5. 조건부 반환: 조건이 있는 여러 'return' 문을 사용하여 입력 또는 논리에 따라 다른 값을 반환할 수 있습니다.

def check_sign(number):
    if number > 0:
        return "Positive"
    elif number < 0:
        return "Negative"
    else:
        return "Zero"

print(check_sign(5))  # Output: Positive

6. Early exit: return 키워드를 사용하면 특정 조건이 충족되거나 오류가 발생하면 나머지 코드를 실행하지 않고 함수를 조기에 종료할 수 있습니다.

def safe_divide(a, b):
    if b == 0:
        print("Division by zero is not allowed.")
        return
    result = a / b
    return result

print(safe_divide(10, 0))  # Output: Division by zero is not allowed. None

7. 반환문 없음: 함수에 반환문이 없으면 묵시적으로 없음을 반환합니다. 이는 작업을 수행하지만 값을 반환할 필요가 없는 함수에 유용합니다.

def print_greeting(name):
    print(f"Hello, {name}!")

result = print_greeting("Alice")
print(result)  # Output: Hello, Alice! None

자주 발생하는 실수들

1. return 문 포함을 잊음
일반적인 실수는 값을 반환할 것으로 예상되는 함수에 return 문을 포함하는 것을 잊는 것입니다. 기본적으로 return 문이 없는 함수는 'None'을 반환합니다. 때문에 값을 반환할 것으로 예상되는 모든 함수에 return 문을 포함해야 합니다.


2. 적절한 형식 없이 여러 값 반환
함수에서 여러 값을 반환할 때 개발자는 때때로 튜플이나 목록과 같은 올바르지 않은 데이터 구조를 사용하기도 합니다. 따라서 다음과 가티 여러 값을 반환할 때 튜플, 목록 또는 사전을 사용하여 리턴 값을 구성해야합니다. 

def multiple_values():
    return 1, 2, 3  # Returns a tuple (1, 2, 3)

3. 리턴 값을 제대로 처리하지 않음
값을 반환하는 함수를 호출할 때 개발자가 리턴 값을 처리하거나 저장하는 것을 잊어버리는 경우가 있습니다. 따라서 함수의 리턴 값을 적절하게 저장하거나 처리해야 합니다.

def add(a, b):
    return a + b

result = add(1, 2)  # Store the return value in a variable
print(result)       # Handle the return value by printing it

4. 조기 루프에서 값 반환
루프를 사용하여 값을 계산할 때 루프 반복이 완료되기 전에 실수로 값을 반환하기 쉽습니다. 따라서 루프를 조기에 중단하려는 경우가 아니면 return 문이 루프 외부에 있는지 확인하십시오.

def sum_of_list(lst):
    total = 0
    for number in lst:
        total += number
    return total  # Return statement outside of the loop

5. 재귀 함수에서 값을 반환하지 않음: 재귀를 사용할 때 호출 스택에 값을 다시 전달하기 위해 return 문을 포함하는 것이 필수적입니다. 이를 잊어버리면 예기치 않은 동작이 발생할 수 있습니다. 따라서 재귀 함수에 return 문을 포함하여 값을 다시 호출 스택으로 전달해야 합니다.

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)  # Return statement in the recursive function

이러한 일반적인 실수와 각각의 솔루션을 알고 있으면 Python 함수에서 반환 값으로 작업할 때 많은 함정을 피할 수 있습니다.

목차

1. 함수와 매개변수
   1. 함수란?
   2. 매개 변수
   3. 자주 발생할 수 있는 실수들
2. 다양한 매개 변수
   
   1. '기본' 매개 변수
   2. '가변' 매개 변수
   3. '키워드' 매개 변수

'기본' 매개 변수

기본 매개 변수는 함수 인수에 대한 기본값을 제공하는 데 사용되므로 함수를 호출할 때 선택 사항이 됩니다. 함수가 호출될 때 기본 매개변수에 대한 값이 제공되지 않으면 기본값이 대신 사용됩니다. 기본 매개변수는 일반적인 사용 사례에 적합한 기본값을 제공하여 기능을 보다 유연하고 사용하기 쉽게 만들 수 있습니다.

매개변수의 기본값을 지정하려면 함수를 정의할 때 할당 연산자(=) 뒤에 기본값을 사용하십시오. 기본 매개변수는 함수 정의에서 기본이 아닌(위치) 매개변수 다음에 나열되어야 합니다.

다음은 기본 매개변수의 개념을 설명하는 예입니다.

def greet(name, greeting="Hello"):
    print(f"{greeting}, {name}!")

# 'greeting' 매개변수의 값을 제공하지 않고 함수 호출하기
greet("Alice") # Output: "Hello, Alice!"

# 'greeting' 매개변수에 값을 전달하며 함수 호출하기
greet("Bob", "Hi") # Output: "Hi, Bob!"

이 예에서 greet 함수에는 name(위치) 및 greeting(기본값)의 두 매개변수가 있습니다. greeting 매개변수의 기본값은 "Hello"입니다. greeting 매개변수에 대한 값을 제공하지 않고 greet 함수를 호출하면 기본값 "Hello"가 사용됩니다.


변경 가능한 객체(예: 목록 또는 사전)를 기본값으로 사용하면 이전 답변에서 언급한 것처럼 예기치 않은 동작이 발생할 수 있다는 점에 유의해야 합니다. 이 문제를 방지하려면 None을 기본값으로 사용하고 필요한 경우 함수 내부에 가변 객체를 생성하십시오.


다음은 기본 가변 객체를 적절하게 처리하는 방법의 예입니다.

def add_item(item, items_list=None):
    if items_list is None:
        items_list = []
    items_list.append(item)
    return items_list

이 예에서 items_list 매개변수의 기본값은 None입니다. 함수 내에서 items_list가 None이면 항목을 추가하기 전에 새 목록이 생성됩니다. 이렇게 하면 변경 가능한 기본값을 사용하여 발생하는 예기치 않은 동작을 방지하여 각 함수 호출에 대해 별도의 목록이 생성됩니다. 이 코드를 사용하는 방법은 다음과 같습니다.

# 새 목록에 첫 번째 항목 추가
new_list = add_item("사과")
print(new_list) # 출력: ["사과"]

# 동일한 목록에 두 번째 항목 추가
existing_list = ["바나나"]
new_list = add_item("체리", existing_list)
print(new_list) # 출력: ["바나나", "체리"]

# 동일한 목록에 세 번째 항목 추가
new_list = add_item("데이트", existing_list)
print(new_list) # 출력: ["바나나", "체리", "데이트"]

'가변' 매개 변수

가변 매개변수를 사용하면 함수가 다양한 수의 인수를 허용할 수 있습니다. 변수 매개변수에는 *args 및 **kwargs의 두 가지 유형이 있습니다. 이들은 각각 가변 개수의 위치 및 키워드 인수를 함수에 전달하는 데 사용됩니다.


*args: *args 구문을 사용하면 함수가 임의 개수의 위치 인수를 허용할 수 있습니다. 추가 위치 인수를 튜플로 수집합니다. 예를 들면 다음과 같습니다.

def print_args(*args):
    for i, arg in enumerate(args):
        print(f"Argument {i + 1}: {arg}")

print_args(1, "Hello", 3.14, [1, 2, 3])

Output:

Argument 1: 1
Argument 2: Hello
Argument 3: 3.14
Argument 4: [1, 2, 3]

**kwargs: **kwargs 구문을 사용하면 함수가 임의 개수의 키워드 인수를 허용할 수 있습니다. 추가 키워드 인수를 사전으로 수집합니다. 예를 들면 다음과 같습니다.

def print_kwargs(**kwargs):
    for key, value in kwargs.items():
        print(f"{key}: {value}")

print_kwargs(name="Alice", age=30, city="New York")

Output:

name: Alice
age: 30
city: New York

단일 함수에서 *args 및 **kwargs를 결합하여 위치 및 키워드 인수의 모든 조합을 허용할 수도 있습니다.

def print_all_args(*args, **kwargs):
    for i, arg in enumerate(args):
        print(f"Positional argument {i + 1}: {arg}")
    for key, value in kwargs.items():
        print(f"Keyword argument {key}: {value}")

print_all_args(1, 2, 3, name="John", age=25)

Output:

Positional argument 1: 1
Positional argument 2: 2
Positional argument 3: 3
Keyword argument name: John
Keyword argument age: 25

가변 매개변수는 함수를 정의할 때 유연성을 제공하여 더 재사용 가능하고 적응 가능한 코드를 생성할 수 있도록 합니다.

'키워드' 매개 변수

Python에서 키워드 매개변수는 위치에만 의존하지 않고 매개변수 이름을 사용하여 함수에 인수를 전달하는 방법입니다. 키워드 인수는 각 인수의 목적을 이해하기 쉽기 때문에 함수 호출을 더 읽기 쉽게 만듭니다. 또한 매개변수 이름을 제공하는 한 임의의 순서로 인수를 지정할 수 있습니다.


다음은 키워드 매개변수의 개념을 설명하는 예입니다.

def calculate_area(length, width):
    return length * width

# 위치 인자를 사용하여 함수 호출하기
area_1 = calculate_area(10, 5)  # 출력: 50

# 키워드 인자를 사용하여 함수 호출하기
area_2 = calculate_area(length=10, width=5)  # 출력: 50
area_3 = calculate_area(width=5, length=10)  # 출력: 50

이 예에서 calculate_area 함수에는 length와 width라는 두 개의 매개변수가 있습니다. 함수를 호출할 때 위치 인수(함수 정의의 매개변수와 동일한 순서로 값을 제공하여) 또는 키워드 인수(매개변수 이름 및 해당 값을 제공하여)를 사용할 수 있습니다. 키워드 인수는 어떤 값이 어떤 매개변수에 해당하는지 명확하게 하며 어떤 순서로든 제공될 수 있습니다.


키워드 매개변수는 함수에 기본값이 있는 여러 매개변수가 있을 때 특히 유용합니다. 앞의 모든 매개변수에 대한 값을 제공하지 않고도 특정 매개변수에 대한 값을 제공할 수 있습니다. 예를 들어:

def print_details(name, age=0, city="Unknown"):
    print(f"Name: {name}, Age: {age}, City: {city}")

# 위치 인자와 키워드 인자를 혼용하여 함수 호출하기
print_details("Alice", city="New York")  # 출력: "Name: Alice, Age: 0, City: New York"

이 예에서 print_details 함수에는 name(위치), age(기본값) 및 city(기본값)의 세 가지 매개변수가 있습니다. 함수를 호출할 때 키워드 인수를 사용하여 age 매개변수에 대한 값을 제공할 필요 없이 이 경우 city와 같은 특정 매개변수에 대한 값을 제공할 수 있습니다.

목차

1. 함수와 매개변수
   1. 함수란?
   2. 매개 변수
   3. 자주 발생할 수 있는 실수들
2. 다양한 매개 변수
   
   1. '기본' 매개 변수
   2. '가변' 매개 변수
   3. '키워드' 매개 변수

함수란?

Python의 함수는 특정 작업을 수행하는 재사용 가능한 코드 블록입니다. 입력 인수(있는 경우)를 사용하고 일련의 작업을 수행하며 출력(있는 경우)을 생성합니다. 다음은 두 개의 숫자를 입력으로 받아 함께 더하고 결과를 반환하는 간단한 함수의 예입니다.

def add_numbers(x, y):
    sum = x + y
    return sum

이 예에서 add_numbers는 함수의 이름이고 x와 y는 입력 인수이며 sum은 x와 y의 합계를 저장하는 변수입니다. 'return' 문은 함수의 출력을 지정하며, 이 경우에는 'sum' 값입니다. 해당 함수를 출력하려면 위 사진과 같이 정의된 함수에 값을 넣어 print 할 수 있습니다.

이런 식으로 함수를 정의한 후에는 코드의 어느 곳에서나 함수를 호출하고 설계된 작업을 수행하는 데 사용할 수 있습니다. 예를 들면 다음과 같습니다.

result = add_numbers(5, 3)
print(result)  # Output: 8

이 예에서 add_numbers 함수는 입력 인수 3 과 4가 함께 호출되고 결과(7)은 result 변수에 할당됩니다. 마지막으로 print 문은 result의 값을 콘솔에 출력합니다. 처음 사진처럼 바로 출력하는 방법과 위 사진 처럼 또 다른 변수를 지정해 출력하는 방법 중 편한 방법으로 사용하면 될 것 같습니다.

매개 변수

Python에서 매개변수는 함수가 호출될 때 함수에 전달되는 값에 대한 자리 표시자 역할을 하는 변수입니다. 사용자의 필요에 따라 다른 입력 값을 취함으로써 기능을 보다 유연하고 재사용할 수 있습니다. 함수가 호출될 때 함수에 전달되는 실제 값을 인수라고 합니다.

다음은 매개변수의 개념을 설명하는 예시입니다.

def greet(name): # 'name' 은 파라미터 입니다.
    print(f"Hello, {name}!")

# 다른 인수로 함수 불러오기
greet("철수") # '철수'가 인수입니다.
greet("영희")   # '영희'가 인수입니다.

이 예에서 greet 함수에는 name이라는 단일 매개변수가 있습니다. greet 함수를 호출할 때 name 매개변수를 대체하는 다른 인수("Alice" 및 "Bob")를 전달합니다. 그런 다음 함수는 전달된 인수를 사용하여 인사말 메시지를 인쇄합니다.

자주 발생할 수 있는 실수들

1. 매개변수 이름 철자 오류
함수 내에서 철자가 틀린 매개변수 이름이 사용되는 경우 함수를 호출할 때 오류가 발생하거나 잘못된 동작이 발생할 수 있습니다.

def greet(user_name):  # 올바른 파라미터 이름
    print(f"Hello, {username}!")  # 값 이름에 오타가 있어 NameError가 출력됩니다.
    print(f"Hello, {user_name}!" # 올바른 방법

greet("철수")

2. 함수를 호출할 때 괄호를 잊어버리기
함수를 호출할 때 괄호를 추가하는 것을 잊으면 예상 반환 값이 아닌 함수 개체 자체에 대한 참조가 발생합니다.

def square(x):
    return x * x

result = square  # 괄호가 없습니다.
result = square(4) # 올바른 방법

print(result(4))  # TypeError: 'function' object is not callable가 출력됩니다.
print(result) # 올바르게 출력하는 방법

3. 잘못된 인수 수
인수가 너무 적거나 너무 많은 함수를 호출하면 TypeError가 발생할 수 있습니다. 함수를 호출할 때 올바른 개수의 인수를 제공해야 합니다.

def add(a, b):
    return a + b

result = add(1)  # 두 번째 인수가 없기 때문에 TypeError가 출력됩니다.
result = add(1, 2)

4. 인수 유형을 고려하지 않음
함수에 전달된 인수 유형을 고려하지 않으면 예기치 않은 동작이나 TypeError 또는 AttributeError와 같은 오류가 발생할 수 있습니다. 인수 유형을 확인하고 그에 따라 처리하거나 예상되는 입력 유형을 명확하게 문서화하는 것이 좋습니다.

def greet(name):
    print(f"Hello, {name}!")

greet(123)  # 출력이 될 수 있으나 에러가 발생할 가능성도 있습니다.
greet("Alice") # 올바른 방법

5. 내장 함수 덮어쓰기
실수로 매개변수에 대한 내장 함수와 동일한 이름을 사용하면 예기치 않은 동작이 발생하고 함수 범위 내에서 내장 함수에 액세스할 수 없게 될 수 있습니다.

def power(base, pow):  # power 함수는 pow로 쓰기도 합니다. 때문에 충돌할 가능성이 있습니다.
    return base ** pow

def power(base, exponent):  # 파라미터 'pow'를 'exponent'로 변경해줍니다.
    return base ** exponent

result = power(2, pow(2, 3))  # pow로 지정하고 출력하면 TypeError가 출력됩니다.

6. 함수 인수 수정
목록이나 사전과 같은 변경 가능한 함수 인수를 수정하면 호출자가 원래 개체가 이전 버전을 출력하지 못하는 등 부작용이 발생할 수 있습니다. 이를 방지하려면 변경 가능한 객체를 수정하기 전에 사본을 만들어야 합니다.

def add_item(item, items_list):
    items_list.append(item)
    return items_list

original_list = [1, 2, 3]
result = add_item(4, original_list)
print(original_list)  # Output: [1, 2, 3, 4] (expected output: [1, 2, 3])

* 복사본을 만드는 예시

def add_item(item, items_list):
    new_list = items_list.copy()  # Create a copy of the input list
    new_list.append(item)
    return new_list

original_list = [1, 2, 3]
result = add_item(4, original_list)
print(original_list)  # Output: [1, 2, 3]

7. 변경 가능한 기본 매개변수 사용
목록이나 사전과 같은 변경 가능한 개체를 기본 매개 변수 값으로 지정하면 동일한 변경 가능한 개체가 함수 호출 간에 재사용되기 때문에 의도하지 않은 부작용이 발생할 수 있습니다.

def add_item(item, items_list=[]):
    items_list.append(item)
    return items_list

print(add_item(1))  # Output: [1]
print(add_item(2))  # Output: [1, 2] (expected output: [2])

이 문제를 방지하려면 None을 기본값으로 사용하고 필요한 경우 함수 내부에 변경 가능한 새 객체를 만듭니다.

def add_item(item, items_list=None):
    if items_list is None:
        items_list = []
    items_list.append(item)
    return items_list

8. 위치 및 키워드 인수 순서
위치 인수는 항상 키워드 인수 앞에 와야 합니다. 순서를 섞으면 구문 오류가 발생하거나 값이 매개변수에 잘못 할당될 수 있습니다.

def example_function(a, b, c=0, d=0):
    pass

example_function(1, 2, 3, d=4)  # Correct
example_function(1, b=2, c=3, d=4)  # Incorrect, raises a syntax error

9. 매개변수 이름 충돌
가변 길이 인수 목록(*args 및 **kwargs)을 사용할 때 다른 매개변수의 이름이 매개변수에 전달된 키워드 인수의 이름과 충돌하지 않는지 확인해야합니다.

def example_function(a, b, *args, c=0, d=0, **kwargs):
    pass

example_function(1, 2, 3, 4, c=5, d=6, e=7, f=8)  # 옳은 방법
example_function(1, 2, 3, 4, a=5, b=6, c=7, d=8)  # 틀린 방법으로  a와 b는 앞에서 이미 지정되었습니다.

10. 선택적 매개변수를 처리하지 않음
선택적 매개변수를 사용할 때 선택적 매개변수가 제공되지 않는 경우를 함수가 처리할 수 있는지 확인해야합니다. 'None' 또는 기타 기본값을 확인하고 그에 따라 처리합니다.

def greet(name, greeting=None):
    if greeting is None:
        greeting = "Hello"
    print(f"{greeting}, {name}!")

greet("철수")  # Output: Hello, 철수!
greet("영희", "Hi")  # Output: Hi, 영희!

Python 함수에서 매개 변수를 지정할 때 이러한 일반적인 실수를 인식하고 모범 사례를 따르면 오류를 방지하고 보다 강력하고 유지 관리가 수월한 코드를 작성할 수 있습니다.

나머지는 2편에 올라올 예정입니다!

목차

1. while 기본 사용법
2. while을 for 처럼 사용하기
3. 상태를 기반으로 while 반복문 사용하기
4. 유닉스 타임으로 while 반복문 사용하기
5. break 키워드
6. continue 키워드

while 기본 사용법

while 반복문은 조건이 참(True)인 동안 코드 블록을 계속 실행하는 구조입니다. 조건이 거짓(False)이 될 때까지 코드 블록 내의 문장들을 반복합니다. 이는 일정 조건을 만족할 때까지 반복해야 하는 경우에 유용합니다.

while 반복문의 기본 구조는 다음과 같습니다.

while condition:
    # 실행할 코드

condition에는 참 또는 거짓을 반환하는 표현식이 들어갑니다. 참일 경우에만 코드 블록이 실행됩니다. 다음은 간단한 while 반복문 예시입니다.

count = 0

while count < 5:
    print(count)
    count += 1

이 코드는 count 변수가 5 미만인 동안 반복문을 실행하며, 반복할 때마다 count 변수를 1씩 증가시킵니다. 따라서 이 코드는 0부터 4까지의 숫자를 출력합니다.

while 반복문을 사용할 때는 주의해야 할 점이 있습니다. 조건이 항상 참이 되어 무한 루프에 빠지지 않도록, 반복문 내에서 조건이 거짓이 될 수 있는 상황을 만들어야 합니다. 그렇지 않으면 프로그램이 끝나지 않고 영원히 실행됩니다.

while을 for 처럼 사용하기

while 반복문을 for 반복문처럼 사용할 수 있습니다. 이렇게 하려면 변수를 초기화하고, 조건문에서 해당 변수를 확인한 후, 반복문 내에서 변수를 업데이트해야 합니다.

예를 들어, for 반복문을 사용해 0부터 4까지의 숫자를 출력하는 코드는 다음과 같습니다.

for i in range(5):
    print(i)

이 코드를 while 반복문으로 변환하면 다음과 같습니다.

i = 0
while i < 5:
    print(i)
    i += 1

먼저 i 변수를 0으로 초기화한 후, while 반복문의 조건에서 i가 5 미만인 동안 반복을 수행하도록 합니다. 반복문 내에서 i를 출력하고, i 값을 1씩 증가시킵니다.

for 반복문과 달리 while 반복문에서는 변수 초기화, 조건 확인 및 변수 업데이트를 명시적으로 처리해야 합니다. 그러나 이 방법으로 while 반복문을 for 반복문처럼 사용할 수 있습니다.

상태를 기반으로 while 반복문 사용하기

while 반복문은 조건이 참인 동안 계속해서 코드 블록을 실행합니다. 상태를 기반으로 반복하는 경우, 상태가 변경될 때까지 반복문을 실행하도록 조건을 설정하면 됩니다. 상태 변수를 사용하여 반복문을 제어할 수 있습니다.

다음은 상태를 기반으로 while 반복문을 사용하는 예시입니다.

is_running = True
counter = 0

while is_running:
    print("반복문 실행 중...")

    counter += 1

    if counter == 5:
        print("반복 횟수가 5에 도달했습니다.")
        is_running = False

print("반복문 종료.")

이 예시에서는 is_running이라는 상태 변수를 사용하여 반복문을 제어합니다. is_running이 참인 동안 반복문이 계속 실행됩니다. counter 변수가 5에 도달하면, is_running 값을 거짓으로 변경하고 반복문이 종료됩니다.

상태를 기반으로 반복하는 while 반복문을 사용하면, 특정 상태가 변경될 때까지 계속 실행할 수 있습니다. 이렇게 하려면 조건에 상태 변수를 사용하고, 반복문 내에서 상태를 업데이트하는 로직을 구현해야 합니다.

유닉스 타임으로 while 반복문 사용하기

유닉스 타임(Unix time)은 1970년 1월 1일 00:00:00(UTC)부터 현재까지 경과한 초를 정수로 나타내는 시간 체계입니다. 파이썬에서 time 모듈의 time() 함수를 사용하여 유닉스 타임을 얻을 수 있습니다.

유닉스 타임을 사용하여 while 반복문을 조절하는 방법은 다음과 같습니다.

1. 반복문 시작 전에 time.time()을 호출하여 시작 시간을 기록합니다.
2. while 반복문의 조건에서 현재 시간과 시작 시간의 차이를 계산하여 반복문을 계속 실행할지 결정합니다.

예를 들어, 다음 코드는 유닉스 타임을 사용하여 10초 동안 while 반복문을 실행합니다.

import time

start_time = time.time()  # 시작 시간 기록
duration = 10  # 반복문을 실행할 시간 (초)

while time.time() - start_time < duration:
    print("반복문 실행 중...")
    time.sleep(1)  # 1초 간격으로 반복문 실행

print("반복문 종료.")

이 예제에서는 시작 시간을 start_time 변수에 저장하고, while 반복문의 조건에서 현재 시간과 시작 시간의 차이를 계산하여 10초 동안 반복문을 실행하도록 합니다. 반복문 내에서 time.sleep(1)을 사용하여 1초 간격으로 반복문이 실행되도록 합니다.

유닉스 타임을 사용하여 while 반복문을 조절하려면, 시작 시간을 기록하고 반복문의 조건에서 경과 시간을 확인하는 방식을 사용하면 됩니다.

break 키워드

break 키워드는 반복문을 강제로 종료하는 데 사용됩니다. while 반복문에서 break를 사용하면 현재 실행 중인 반복문을 즉시 종료하고, 반복문 블록 이후의 코드를 실행합니다. break는 종종 중첩된 반복문을 빠져나가거나, 특정 조건이 충족될 때 반복문을 종료할 때 유용합니다.

다음은 while 반복문에서 break 키워드를 사용하는 예시입니다.

counter = 0

while True:
    print("반복문 실행 중...")
    counter += 1

    if counter == 5:
        print("반복 횟수가 5에 도달했습니다.")
        break

print("반복문 종료.")

이 예제에서는 while 반복문의 조건이 항상 참인 True로 설정되어 있습니다. 그러나 반복문 내에서 counter 변수가 5에 도달하면 break 키워드가 실행되어 반복문이 즉시 종료됩니다. 이렇게 break를 사용하면 조건이 참인 동안에도 특정 조건을 만족하면 반복문을 종료할 수 있습니다.

continue 키워드

continue 키워드는 반복문에서 현재 반복을 중단하고, 다음 반복을 시작하는 데 사용됩니다. while 반복문에서 continue를 사용하면, 현재 실행 중인 반복에서 남은 코드를 건너뛰고 다음 반복을 시작합니다. continue는 특정 조건이 충족될 때 해당 반복의 나머지 부분을 건너뛰고 싶을 때 유용합니다.

다음은 while 반복문에서 continue 키워드를 사용하는 예시입니다.

counter = 0

while counter < 10:
    counter += 1

    if counter % 2 == 0:
        continue

    print(f"홀수: {counter}")

print("반복문 종료.")

이 예제에서는 counter가 10 미만인 동안 반복문이 실행됩니다. 반복문 내에서 counter가 짝수인 경우, continue 키워드가 실행되어 현재 반복에서 남은 코드를 건너뛰고 다음 반복을 시작합니다. 따라서 print() 함수는 counter가 홀수인 경우에만 실행됩니다.

이렇게 continue를 사용하면 반복문 내에서 특정 조건을 만족할 때 해당 반복의 나머지 부분을 건너뛰고 다음 반복을 시작할 수 있습니다.

목차

1. for문에 range 함께 사용하기
2. for문에 list, range 함께 사용하기
3. for 역반복문
4. 응용 예시

for문에 range 함께 사용하기

파이썬의 `for` 반복문과 `range()` 함수를 함께 사용하면 특정 범위의 숫자를 반복적으로 처리할 수 있습니다. 다음은 몇 가지 예시입니다.

1. 0부터 9까지의 숫자를 출력하는 예시:

for i in range(10):
    print(i)

2. 1부터 10까지의 숫자를 출력하는 예시:

for i in range(1, 11):
    print(i)

3. 0부터 8까지의 짝수를 출력하는 예시:

for i in range(0, 10, 2):
    print(i)

4. 1부터 10까지의 숫자의 제곱을 출력하는 예시:

for i in range(1, 11):
    print(i**2)

5. 1부터 10까지의 짝수를 출력하는 예시:

for i in range(2, 11, 2):
    print(i)

`for` 반복문과 `range()` 함수를 함께 사용하면 이처럼 다양한 범위와 조건에 따라 숫자를 반복적으로 처리할 수 있습니다.

for문과 list, range 함께 사용하기

`for` 반복문, `list`, 그리고 `range()`를 함께 사용하는 예시를 들어보겠습니다. 이 예시에서는 각 학생의 점수를 저장한 리스트와 학생 번호를 `range()` 함수로 생성한 후, 각 학생의 점수를 출력합니다.

# 학생들의 점수 리스트
scores = [95, 88, 76, 89, 53]

# 학생 수에 맞춰 학생 번호 생성
num_students = len(scores)

# 학생 번호와 점수를 함께 출력
for i in range(num_students):
    print(f"학생 {i+1}의 점수: {scores[i]}")

이 코드는 `range()` 함수를 사용하여 학생 번호를 생성하고, `for` 반복문을 사용하여 각 학생의 점수를 리스트에서 가져와 출력합니다.

for 역반복문

for 역반복문은 시퀀스를 거꾸로 반복하는 것을 의미합니다. 파이썬에서는 `reversed()` 함수를 사용하여 역반복문을 수행할 수 있습니다. `reversed()` 함수는 시퀀스를 거꾸로 뒤집어 역반복을 가능하게 합니다.

다음은 몇 가지 역반복문 예시입니다.

1. `reversed()`와 `range()`를 사용한 역반복문:

for i in reversed(range(5)):
    print(i)

이 코드는 4부터 0까지의 숫자를 출력합니다.

2. 리스트를 사용한 역반복문:

fruits = ["apple", "banana", "cherry"]
for fruit in reversed(fruits):
    print(fruit)

이 코드는 리스트의 요소를 역순으로 출력합니다.

또한, `range()` 함수의 세 번째 인자를 음수로 설정하여 역반복문을 수행할 수도 있습니다. 예를 들어, 10부터 1까지 역순으로 출력하려면 다음과 같이 작성할 수 있습니다.

for i in range(10, 0, -1):
    print(i)

이렇게 `for` 반복문과 `reversed()` 함수 또는 음수 간격을 사용하면 파이썬에서 역반복문을 쉽게 수행할 수 있습니다.

응용예시

다음은 `for` 반복문을 사용하여 피라미드 모양을 출력하는 예시입니다. 이 예시에서는 피라미드의 높이를 5로 설정하였습니다.

height = 5

for i in range(height):
    spaces = ' ' * (height - i - 1)  # 공백 출력을 위한 문자열
    stars = '*' * (2 * i + 1)  # 별(*) 출력을 위한 문자열
    print(spaces + stars)

이 코드는 다음과 같은 피라미드를 출력합니다.

    *
   ***
  *****
 *******
*********

피라미드의 높이를 변경하고자 하는 경우, `height` 변수의 값을 변경하면 됩니다.